 In Ontario in our grade
In Ontario in our grade 12 advanced functions course we are to graph rational functions that are reciprocals of linear and quadratic functions and ones where both the numerator and denominator are linear functions. In this post there are several activities (both hands on and electronic) that could be used throughout a unit on graphing Rational Funcitons. Here, we start with an investigation that is done with students in groups graphing reciprocal linear and quadratic functions by hand and then ends with a Desmos Card sort. There is also a Desmos investigation on functions in the form
- MHF4U 2.1 - determine, through investigation with and without technology, key features (i.e., vertical and horizontal asymptotes, domain and range, intercepts, positive/negative intervals, increasing/decreasing intervals) of the graphs of rational functions that are the reciprocals of linear and quadratic functions, and make connections between the algebraic and graphical representations of these rational functions.
- MHF4U 2.2 - determine, through investigation with and without technology, key features (i.e., vertical and horizontal asymptotes, domain and range, intercepts, positive/negative intervals, increasing/decreasing intervals) of the graphs of rational functions that have linear expressions in the numerator and denominator, and make connections between the algebraic and graphical representations of these rational functions
- MHF4U 2.3 - sketch the graph of a simple rational function using its key features, given the algebraic representation of the function
- Chart paper or vertical surfaces for the investigation (markers etc)
- If you choose to do the hands on card sort then you need to make copies of this set of cards (one per group). We usually make these on card stock and laminate them for durability.
- If you choose to do the Desmos card sort then you need to have technology for your students.
Activity 1: Reciprocal linear and quadratic functions
- Put students in groups of no more than three. They can work on vertical surfaces or at a table.
- Each group is given one set of a linear equation and its corresponding reciprocal (or rational) function. There is enough sets for 11 groups. They are to graph each on the same axis. Afterwards they should determine any intercepts and/or equations of asymptotes (see answers to the right).
- Once complete they should walk around the class to see other sets and come to some conclusions as to properties of linear functions and their corresponding rational functions.
- Once complete there is a couple of follow up questions to check their thinking.
- Next each group gets a set of quadratic functions and corresponding rational function. They are to graph each on the same axis. Afterwards they should determine any intercepts and/or equations of asymptotes.
- Again, once complete, they should walk around the class to see other sets and come to some conclusions.
- There is another set of follow up questions to check their thinking (note, if time is a problem students can do a similar investigation for homework with this Desmos activity instead of the above steps).
- As a follow up (maybe next day) you can do this physical card sort or this Desmos card sort. The Desmos card sort has some follow up questions to consolidate some of the ideas.

Activity 2 Graphs in the form 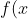=&space;\frac{ax+b}{cx+d})

- Students complete the Desmos Investigation. This can be done in class or as a homework assignment.
- As consolidation, students can check what they know with this quiz. This can be done using paper and pencil (copy double sided then cut in half) or via this online Google Form. Note that if you use the form, click on this link and then choose advanced options (3 vertical dots) to make a copy. Please do not edit our form.
Activity 3: Desmos MarbleSlides for 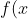=&space;\frac{ax+b}{cx+d})
- To show if they understand the investigation from Activity 2, students can complete this Desmos MarbleSlides. The first few slides are just to show some possible solutions and then the challenges start. Note that students may have to work with the domain of the function to become successful.
If you want to know how to create your own Marbleslides, watch this video
Activity 4: Which One Doesn't Belong Assignment
- As a review you might choose to assign students to create their own Which One Doesn't Belong (https://talkingmathwithkids.com/wodb/). The goal here is to create four graphs such that each of the graphs could be chosen as the one that doesn't belong based on specific criteria.
- Activity 1 Investigation (PDF, Google Doc, Desmos)
- Activity 1 Card Sort (PDF, Google Doc, Desmos)
- Activity 2 Investigation (Desmos)
- Activity 2 Homework Quiz (PDF, Google Doc, Online form - make a copy, don't edit ours)
- Activity 3 Marble Slides (Desmos)
- Activity 4 Which One Doesn't Belong (PDF, Google Doc)




No comments:
Post a Comment