Geometer's Sketchpad - Practice Distance Between Points

When using the Geometer's Sketchpad it is often better to "start from sketch, not from scratch". That is, give students a premade sketch rather having them build something from nothing (as many textbooks would have you do). In this activity students can download a GSP sketch that allows them to practice determining the distance between two points (this part could also be used to check answers) and then to be quizzed with randomly generated sets of points.

• MPM2D - develop the formula for the length of a line segment, and use this formula to solve problems (e.g., determine the lengths of the line segments joining the midpoints of the sides of a triangle, given the coordinates of the vertices of the triangle, and verify using dynamic geometry software);

• All that is needed are the electronic downloads
• Note that this really works well on an iPad using the Sketchpad Explorer App (which is free)
• You can also use this on any web based computer (or Chromebook) with this Web sketch

Watch the video below to see how to use the sketch. The first page can be used for discovery or for checking problems and the second page can be used for quizzing students as it will generate an infinite number of random points to find the distance between.

• DistancePractice.gsp (iPad/V5) (V4)
• Web sketch here
• For more sketches like this go to my full page

Did you use this activity? Do you have a way to make it better? If so tell us in the comment section. Thanks

Sort Students into Groups using Linear Representations

In this activities students are each given one card. The card will either have a graph, table of values or equation of a linear relation. Their job is to find the two other students who have the other two representations of the same linear relationship. This shouldn't take too long and could be repeated every couple of days to solidify conversion between representations

MPM1D, MFM2P  - 

• graph lines by hand, using a variety of techniques
• identify, through investigation with technology, the geometric significance of m and b in the equation y = mx + b

• Download the cards and cut them out (you may want to laminate them)

1. Shuffle the cards and distribute one per student. Note that there are 11 sets of 3 cards so you may want to remove sets to more closely match your student population.
2. Students will find the other people who have the same linear relationship

• GraphTableLineMatch (doc) (pdf)

Did you use this activity? Do you have a way to make it better? If so tell us in the comment section. Thanks

Halloween Proportional Reasoning Review Activity

This is a Halloween review activity where students will answer proportional reasoning questions and collect candy on the Smartboard (This is the Halloween version to an Easter activity post. If teaching in the fall this context makes more sense otherwise in the spring use the Easter activity instead at this link - they are the same questions in both activities)

MFM1P 

• illustrate equivalent ratios, using a variety of tools (e.g., concrete materials, diagrams, dynamic geometry software) 
• represent, using equivalent ratios and proportions, directly proportional relationships arising from realistic situations
• solve for the unknown value in a proportion, using a variety of methods
• make comparisons using unit rates – solve problems involving ratios, rates, and directly proportional relationships in various contexts using a variety of methods
• solve problems requiring the expression of percents, fractions, and decimals in their equivalent forms

• 49 Halloween containers (find at a Dollar store)
• proportional reasoning questions
• solution handout
• Smartboard
• Smart Notebook file with score board
• whiteboard and markers (optional)
• Halloween decorations (optional)
• prizes for winning team (optional)

1. Cut out questions and place one in each of the 49 containers.
2. Spread out containers on a table and add some Halloween decorations (optional).
3. Bring up the scoreboard on the smartboard.  (Could create your own scoreboard if a smartboard is not available)
4. Place students is groups and give each student a whiteboard and marker.
5. Have each group choose a Halloween bag from the scoreboard.
6. One student from the group will come up and choose a container.  They will bring it back to their group where all members will answer the question inside.
7. One person will then come and check their answer with the teacher.
8. The teacher will check off that the group has answered that question.  
9. The student will then drag a candy to their bag on the smartboard.  Questions with no pumpkins are worth 1 candy and questions with 2 pumpkins are worth 2 candies.
10. Have students place the question back in the container and choose another one.  (Answered questions with container should be put to the side and put back in circulation when containers get low.)
11. The group who collects the most candy will win.  

Note:  There are some special cards that students will find. Tap bags 1, 3, 6 or 8 on the Smartboard to play Halloween music.

The video, below, is only visible in the WECDSB domain. That is, only teachers in our school board can see the video if they are logged into their MyTools2Go accounts.

• Proportional Reasoning Halloween questions (pdf) (doc)
• Proportional Reasoning Halloween solutions (pdf) (doc)
• Halloween scoreboard (Smart Notebook file) (not)

Did you use this activity? Do you have a way to make it better? If so tell us in the comment section. Thanks

How do I compare to Michael Phelps?

When talking about linear relationships and scatter plots, a common activity is to have students measure their various body parts and then compare sets of them to see if there is a correlation. This activity builds on an activity in the TIPS package for grade 9 Applied (Section 3.1.2-4 pg 4). Kids usually like that activity (probably since they get to move around). This is a small tweak to make that activity a little more engaging. In this activity, students compare their arm span, foot size and hand size to some unknown people (arm span is Michael Phelps, foot size is Shaquille O'Neal, hand size is Michael Jordan - yes some still know who he is) and the heights of the tallest and shortest humans (among others).

• MFM1P, MPM1D – B1.4 describe trends and relationships observe in data, make inferences from data, compare the inferences with hypotheses about the data, and explain any differences between the inferences and the hypotheses
• MDM4U - D2.3 generate, using technology, the relevant graphical summaries of two-variable data (e.g., scatter plots, side-by-side boxplots) based on the type of data provided (e.g., categorical, ordinal, quantitative)
• MAP4C - D1.3 generate, using technology, the relevant graphical summaries of two-variable data (e.g., scatter plots, side-by-side boxplots) based on the type of data provided (e.g., categorical, ordinal, quantitative); D1.4 generate, using technology, the relevant graphical summaries of two-variable data (e.g., scatter plots, side-by-side boxplots) based on the type of data provided (e.g., categorical, ordinal, quantitative) 

The material set up for this one is a bit labour intensive. There are some that require taping multiple sheets together

• Michael Phelps - this is probably the hardest to pull off. We took this image of Phelps and wanted to blow it up so that it's arm span matches his actual arm span of 6'7" (201cm). To do this we changed the contrast so that the face was less recognizable then used the Poster Razer to slice the image up into 8 pieces (this is actually a free program that is great for making large posters out of smaller pieces of paper). We then printed them on 31"x23" poster sheets and then taped them together and laminated them.

• Shaquille O'Neal - Shaq's feet come in two pieces that have to be taped together
• Michael Jordan - No special instructions for the hands
• Height Wall - We have provided for you some samples to include on the height wall, including some really tall and really short ones and some popular culture examples. We encourage you to add your own examples (ones that resonate with your own students). Cut these out to be placed on the height wall for students to see and compare to.
• Other materials that you will need are measuring devices (metre sticks, measuring tapes etc) 

1. Prior to students arriving in class, tape the feet to the floor at the classroom entrance, tape the hands on the wall where they will be visible, tape the arm span on the wall so there is room for kids to measure up to it and find a spot to make your height wall. The height wall should have a measuring tape on it (or metre sticks) so students can measure themselves but also stick the sample heights of the famous people on the wall to have students compare to them.
2. As a Minds On you might want to show this image and ask "How tall would the person be to fit this shoe?"
3. Students start by completing p. 4 from TIPS.
4. Students record their measurements on p. 5 and as they circulate they can compare their own measurements to those on the walls and floor. Along the way they can make guesses as to who the mystery feet, hands and arm span are.  
5. Collect students' data
6. Ask students to reveal their guesses.  Have them discuss why they chose these people.
7. Invite students to add there own person to the height wall.
8. As an extension, you can collect this data in a spreadsheet or online form. We have created a sample Google form (or use this link http://bit.ly/relationshipform). If you want your own copy, contact us and we will share one with you. Here is a link to the spreadsheet of data. When you use this form be sure to have students put in a unique class identifier so that you can find your class data in our spreadsheet of data.  
9. You can analyse the data with students using Fathom. (What is the best predictor of your height? Is your foot length the same as your forearm length?)
10. Some extension material on Michael Phelps can be found in this Smart Notebook file and this documentary called Miracle Body.

• Scans of the feet and hands (pdf) - note Phelps is light here and you can recognize him
• Scans of arm span posterized (pdf)  - this is a darker scan of just the arm span pieces.
• Michael Phelps original image (Dark) (Light)
• Michael Phelps info File (not) (pdf)
• Height Wall (doc) (pdf)
• TIPS Activity (doc) (pdf)

Did you use this activity? Do you have a way to make it better? If so tell us in the comment section. Thanks

An Open Sort dealing with Similarity and Congruence

In this activity students are given a card that has some sort of image on it. This is an open sort. That is students are then asked to sort themselves with no other instructions. Teachers are often leery of this type activity (with so few instructions) because they are worried that it might not go the way they want. Sometimes that is true but most times kids will do alright. And they need opportunities to think freely about math without the burden of assessment. This is a great way to do it.
New: Alternatively, you could have students just work individually on this Desmos card sort

• Gr7GS - distinguish between and compare similar shapes and congruent shapes, using a variety of tools
• Gr8GS - determine, through investigation using a variety of tools (e.g., dynamic geometry software, concrete materials, geoboard), relationships among area, perimeter, corresponding side lengths, and corresponding angles of similar shapes.

Set of Open Sort cards. There are 21 all together so you may need two sets if you have a bigger class. Print them on card stock, cut them out and laminate (optional)

1. Each student is given a card 
2. Ask students to sort themselves out using any criteria they wish
3. If sorting isn't happening in the way you wish, you may want to take some of the openness away and give them a bit more instruction.

The videos, below, are only visible in the WECDSB domain. That is, only teachers in our school board can see the video if they are logged into their MyTools2Go accounts.

• Open Sort Similarity Cards (pdf) (doc)

Did you use this activity? Do you have a way to make it better? If so tell us in the comment section. Thanks

Tarsia Puzzle - Multiplying and Dividing by powers of 10

We came across these puzzles a few years ago. The premise is that you have a bunch of questions and matching answers. Students have cards that have either an answer or question on the edge. They then have to match up the edges that have the pairs of questions and answers and eventually it will make a shape. In this case the activity is matching up different representations of the same number.
We found these puzzles originally on the Mr Barton Maths site under the Tarsia Jigsaw Page. The nice thing here is the Tarsia software can be downloaded here (click the green button to download - unfortunately it is Windows only) and you can edit or create your own puzzles. So this puzzle was one of our creations. There are even banks of hundreds of already created puzzles on the site (just scroll down on the Tarsia page and look for the smiley faces for zipped files). These are great puzzles to pull out when you want to break up a long class or have 10 min at the beginning or end of a class to fill.

• Gr8NS - multiply and divide decimal numbers by various powers of ten

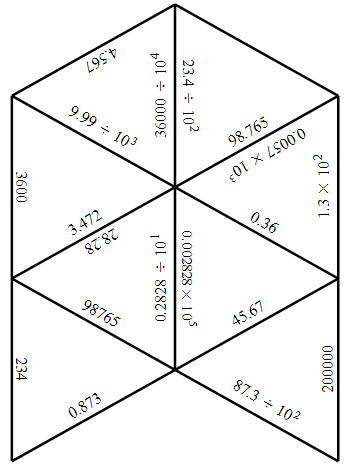
Tarsia Card Prep work: There are two downloads (three if you include the actual Tarsia file). The actual cards for the puzzle and the answer card. The cards for the puzzle come on 2-4 sheets (there are different styles of puzzles) and each triangle needs to be cut out (see image tot the right). We have found that if you have several sets of the same puzzle (say if students do it in groups of 3) then it is best to copy each set in a different colour. That way it is harder to get the sets mixed up and easier for clean up after (ie you only need to check if there are 18 cards of each colour). We find that the cards last longer if you laminate them first then cut them.

1. This activity can be done in groups or individually and can take about 15 min depending on the student.
2. Hand students the entire set and ask them to match up the different representations of the same number.  The outside edges are blank.
3. In this case the finished puzzle looks like a hexagon.

• Note: this puzzle is challenging because many of the questions have the same digits.

• Multiplying and Dividing decimals by powers of 10 Tarsia cards (pdf)
• Multiplying and Dividing decimals by powers of 10 Tarsia solution (pdf)
• Multiplying and Dividing decimals by powers of 10 Editable (xjsw)

Did you use this activity? Do you have a way to make it better? If so tell us in the comment section. Thanks

Integer Multiplication Mind Reader

This one is pretty simple but the students seem to really like it. We got the idea from a colleague and am sure we aren't the first to do it. Basically you get groups of three. Two students grab a card from a deck and without looking at them put them on their foreheads facing out. The third student multiplies the two numbers and states the product. Those holding the cards then try to guess the two numbers.

• Gr8NS - represent the multiplication and division of integers, using a variety of tools 
• MPM1D - As review
• MFM1P - As review

• All that is needed are decks of cards. Here black cards are positive and red cards are negative (or vise versa if you prefer). You may wish to remove the face cards or come up with protocol for which numbers the face cards represent. On side note, if you use the face cards, don't assume that all students will know what a face card is (ie a card that literally has a face on it) as it seems that more and more students may not have the experience of playing cards at home. 
• Optional materials might be a personal portable white board and dry erase marker for students.

1. Create groups of three students. 
2. In the group choose 2 mind readers and one product leader
3. Each mind reader chooses a card and without looking at either card, place them face out on their foreheads. 
4. The product leader multiplies the two integers (red is negative, black is positive) and states the product (or writes it on their whiteboard)
5. The mind readers then take turns guessing the factors (cards) they are holding).
6. The first to guess correctly becomes the new product leader and the original product leader becomes a mind reader. 
7. Repeat as often as you wish

• Integer Mind Reader Instructions (pdf)

Did you use this activity? Do you have a way to make it better? If so tell us in the comment section. Thanks